Apêndice C – Solução de sistemas de equações lineares
Introdução
O problema que pretendemos resolver neste apêndice é como determinar o valor de x ∈ Rn tal que Ax = b, sendo b ∈ Rn e A ∈ Mn(R), onde Mn(R) denota o conjunto das matrizes reais de ordem n. Para resolver esse problema, iremos supor que a matriz A é invertível ou, o que é equivalente, que o sistema é possível e determinado. Um sistema de equações lineares pode ser escrito da seguinte forma:
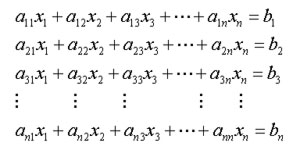
Em forma matricial:
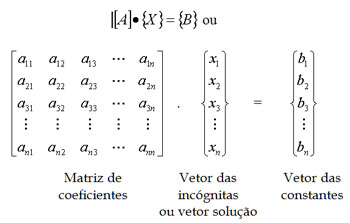
A resolução de um problema que envolve sistemas lineares divide-se em três etapas:
1. formulação do modelo matemático (calcular a matriz A);
2. cálculo dos agentes exteriores (calcular o vetor b);
3. resolução do sistema linear.
Os dois primeiros passos dependem, obviamente, do conhecimento do problema físico (tipo de material, leis físicas etc); o terceiro passo pode ser equacionado e resolvido separadamente, por meio de um algoritmo matemático conveniente. Uma vez que esse último passo aparece como pertencente a um algoritmo bastante mais vasto, é essencial que seja calculado de forma eficiente.
Existem duas grandes classes de métodos para resolver sistemas de equações lineares: os métodos diretos, que já foram estudados, dos quais faremos uma breve revisão; e os métodos iterativos, que iremos estudar com mais detalhes, especialmente os de Carl Gustav Jakob Jacobi (1804-1851), Johann Carl Friedrich Gauss (1777-1855) e Philipp Ludwig von Seidel (1821-1896). Antes, porém, vamos apresentar algumas classes de matrizes que serão consideradas.
Classes de matrizes
Existem vários tipos de matrizes com relevância em aplicações práticas:
• Matrizes densas e esparsas. Uma matriz com muitos elementos nulos chama-se esparsa; caso contrário, é densa. Como caso particular das matrizes esparsas, há as matrizes banda e, dentro dessa classe, há as chamadas matrizes tridiagonais. As matrizes banda são aquelas cujos elementos não nulos se concentram apenas em um conjunto de diagonais paralelas à diagonal principal;
• Matrizes triangulares. As matrizes triangulares possuem todos os seus elementos acima ou abaixo da diagonal principal iguais a zero. No primeiro caso, as matrizes são chamadas de triangulares inferiores e no segundo, de triangulares superiores.
• Matrizes simétricas. As matrizes simétricas coincidem com a sua transposta. Uma característica importante dessas matrizes é o fato de que todos os seus valores próprios são reais.
• Matrizes estritamente diagonais dominantes (EDD). Uma matriz ![]() é estritamente diagonal dominante por linhas se:
é estritamente diagonal dominante por linhas se:
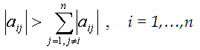
e estritamente diagonal dominante por colunas se:
![]()
A matriz é estritamente diagonal dominante se for estritamente diagonal dominante por linhas ou colunas.
• Matrizes simétricas e positivas definidas (SPD). Uma matriz é chamada simétrica e positiva definida se for simétrica e se, para todo o vetor x ∈ Rn, não nulo, tem-se xTAx > 0.
Métodos diretos
Consideremos, de novo, o problema de determinar o vetor x ∈ Rn tal que Ax = b, sendo b ∈ Rn e A ∈ Mn(R). O primeiro tipo de método que iremos considerar para resolver esse problema é o chamado método direto. Esse método nos permite obter a solução exata do problema em um número finito de operações aritméticas, supondo não haver erros de arredondamento ou quaisquer outros.
Os métodos diretos baseiam-se no processo de eliminação de Gauss, que consiste em transformar o sistema Ax = b em um sistema equivalente Ux = c, onde U é uma matriz triangular superior, por meio de operações elementares efetuadas na matriz de coeficientes (A). O sistema a resolver pode ser escrito na forma:
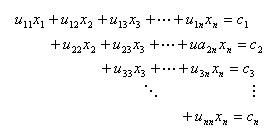
e a sua resolução, caso , uii ≠ 0, i = 1, . . . , n, é feita de acordo com o algoritmo seguinte.
Algoritmo C.1 Resolução de um sistema triangular superior
Dados: ci, i = 1, . . . , n, e uij, i = 1, . . . , n, j = i, . . . , n
xn = cn/unn
Para i de n - 1 até 1 fazer
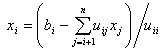
Resultado: xi , i = 1, . . . , n
A desvantagem do método da eliminação de Gauss é a alteração do valor dos termos independentes ( ). Para contornar esse problema, há o chamado método da triangulação, que consiste em decompor a matriz A do sistema a ser resolvido na forma:
A = L U
onde L é uma matriz triangular inferior, e U uma matriz triangular superior, com uii = 1, i = 1, . . . , n. A forma de se obter essa decomposição é conhecida como decomposição de Gauss. Depois de obtida a decomposição, a resolução do sistema é feita em duas etapas: resolver Ly = b; resolver Ux = y. Note que em cada etapa há um sistema triangular a ser resolvido.
Algoritmo C.2 Resolução de um sistema triagonal
Dados: matriz A e vetor b
Determinar as matrizes L e U
% Resolver Ly = b
y1 = b1/l1
Para i de 2 até n fazer
yi = (bi - aiyi - 1)/li
% Resolver Ux = y
xn = yn
Para i de n - 1 até 1 fazer
xi = yi - uixi + 1
Resultado: xi, i = 1, . . . , n
Teorema C.1 Para uma matriz A ∈ Mn(R), a decomposição LU existe
e é única se e só se as submatrizes principais de A forem não singulares.
Note-se que, se A ∈ EDD ou a ∈ SPD, a matriz A verifica as hipóteses do teorema anterior e, como tal, a decomposição LU de A existe e é única.
Mais ainda, se A ∈ SPD, a decomposição de A pode ser obtida na forma A = HHT , onde H é uma matriz triangular inferior com elementos diagonais positivos. Essa decomposição é conhecida como decomposição de Cholesky.
Quando, no processo da decomposição de Gauss, encontramos uma linha nula, podemos trocar de linha, de forma a evitar uma divisão por zero. Uma possibilidade é escolher, em cada passo da iteração, uma linha de módulo máximo. Consegue-se, assim, a decomposição PA = LU, onde P é a matriz de permutação da linha efetuada.
Métodos iterativos
Consideremos, mais uma vez, o problema de determinar o valor de x ∈ Rn tal que Ax = b, sendo b ∈ Rn e A ∈ Mn.(R) uma matriz invertível. Um método iterativo para resolver o sistema é partir de uma aproximação inicial x(0) para a solução do sistema (que iremos denotar por x*), gerando uma sucessão de vetores {x(k)} convergente para x*. Os métodos que iremos considerar pertencem à classe dos métodos do ponto fixo e são obtidos pela transformação do problema Ax = b em um outro, equivalente, na forma:
x = Bx + g
para uma determinada matriz de iteração B e um determinado vetor g. Para determinar B e g, podemos, por exemplo, decompor a matriz A na forma:
A = P (P - A)
sendo P uma matriz invertível (mais simples que A), chamada pré-condicionador, e considerar:
B = P-1(P - A) e b = P-1g
De fato,
Ax = b ⇔ Px = (P - A)x - b ⇔ x = P-1 (P - A)x + P-1b
Com essa transformação, podemos escrever o método iterativo na forma:
x(0), dado,
x(k+1) = B . x(k) + g, para k = 0, 1, 2, ...
Atendendo a:
x(k+1) = B . x(k) + g ⇔ Px(k+1) = (P - A).x(k) + b ⇔ P( x(k+1) - x(k)) = b - A.x(k)
O processo iterativo termina quando se cumprirem os critérios de parada estabelecidos.
Os critérios mais comuns são:
1. Critério do erro absoluto: ||x(k) - x(k-1)|| ≤ ε;
2. Critério do erro relativo: ||x(k) - x(k-1)|| ≤ ε ||x(k)||;
3. Critério do número máximo de iterações: k = kmáx.
Os métodos iterativos são, sobretudo, usados para matrizes esparsas de grandes dimensões, que surgem frequentemente em problemas de recursos hídricos. Para esses problemas, os métodos iterativos são competitivos, em comparação com os métodos diretos. Para matrizes densas ou de pequena dimensão, os métodos diretos são mais vantajosos.